Movie: Shape flow for a 2D rod towards optimal reliability.
As three working groups (Optimization, High Performance Computing and Stochastics) at the IMACM in Wuppertal, we develop probabilistic shape optimization models for different failure mechanisms, notably for low cycle fatigue (LCF) problems, with gradient based methods. Low cycle fatigue is a surface driven failure mechanism that occurs under cyclic loading of technical units made of polycrystalline metal. To calculate the shape gradients, we discretize the component via finite elements and then use an adjoint approach.
Objective functions based on the peak stress that stem from mechanical integrity are in general not differentiable, since the component always deterministically fails at the point with the lowest longevity and the highest loading. So we replace the deterministic approach by a probabilistic approach to enable the calculation of shape gradients (sensitivities). With these sensitivities we are able to apply gradient based optimization using an adjoin approach without compromising the structural integrity. In our work we focus on 3D turbo-machinery components, i.e. LCF problems, and 2D ceramic geometries under tensile load.
In these settings, we can assume that the material follows a linear isotropic material law. Thus we can constrain our problem with the usual state equation of linear elasticity in the weak formulation with cyclic or mixed Dirichlet-Neumann boundary conditions. The analysis of the probability of failure (PoF) leads to Weibull type objective functionals allowing us to calculate the shape derivatives. We then first discretize the problem via finite elements and then use the Lagrangian approach to avoid the “curse of dimension”.
To solve the state equation and for calculating the adjoint state, the finite element solver ABAQUS is used for the LCF case. To validate the computation we first calculated the shape gradients for a predictable geometry, in this case a bended rod ( Figure 1) which is fixed at the left-hand boundary and surface forces act on the right-hand boundary. With this preliminary case study, we were able to apply our approach to a 3D aero gas turbine 1st stage compressor blisk model (Figure 2).

Figure 1: Shape derivative towards lower fatigue failure probability for a bended rod
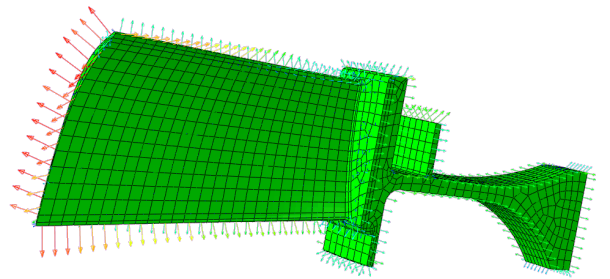
Figure 2: Shape derivative towards higher fatigue failure probability for a turbine blisk geometry under centrifugal load
We also applied this approach to simple 2D ceramic geometries. We were able to construct shape flows to improved shapes in these cases. Throughout this work it became clear that multi-objective optimization would be a desirable extension as the minimization of PoF may lead to shapes that have a poor performance in other relevant criteria, like for example efficiency, volume and costs. The first results of this multi-objective optimization for a 2D ceramic case study with objective functions PoF and material consumption (volume), i.e. a part of the Pareto-front of shapes with a tradeoff between these objectives, is shown in Figure 3.
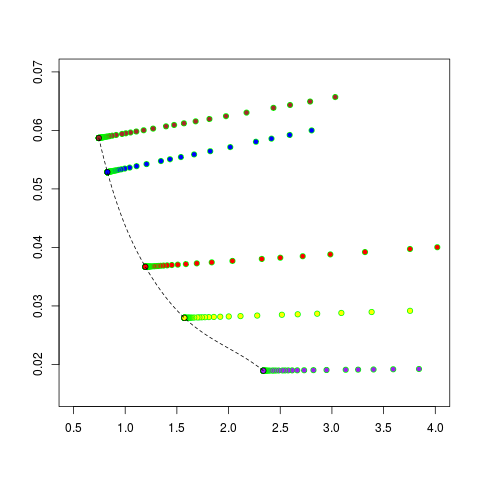
Figure 3: Approximate Pareto front for a 2D bended rod with (negative, logarithmic) probability of survival (x-axis) and material consumption (y-axis) as objective functions
In the upcoming GIVEN collaboration with V. Schulz at U Trier, Siemens Energy and DLR Cologne and also the numerics group (M. Ehrhardt and M. Günther) at BUW, we will extend this multi-objective results to 3D LCF models where the objectives PoF and aerodynamic efficiency, which is computed using adjoint CFD turbo machinery solver TRACE, are considered and integrated to a multicriteria gradient based 3D optimization process.
- Matthias Bolten
- Onur Tanil Doganay
- Hanno Gottschalk
- Camilla Hahn
- Kathrin Klamroth

.png)
